In the last blog post, I took a closer look at how the Extended Triple Diffie-Hellman Key Exchange (X3DH) is used in OMEMO and which role PreKeys are playing. This post is about the other big algorithm that makes up OMEMO. The Double Ratchet.
The Double Ratchet algorithm can be seen as the gearbox of the OMEMO machine. In order to understand the Double Ratchet, we will first have to understand what a ratchet is.
Before we start: This post makes no guarantees to be 100% correct. It is only meant to explain the inner workings of the Double Ratchet algorithm in a (hopefully) more or less understandable way. Many details are simplified or omitted for sake of simplicity. If you want to implement this algorithm, please read the Double Ratchet specification.

Image by Benedikt.Seidl [Public domain]
A ratchet is a tool used to drive nuts and bolts. The distinctive feature of a ratchet tool over an ordinary wrench is, that the part that grips the head of the bolt can only turn in one direction. It is not possible to turn it in the opposite direction as it is supposed to.
In OMEMO, ratchet functions are one-way functions that basically take input keys and derives a new keys from that. Doing it in this direction is easy (like turning the ratchet tool in the right direction), but it is impossible to reverse the process and calculate the original key from the derived key (analogue to turning the ratchet in the opposite direction).
Symmetric Key Ratchet
One type of ratchet is the symmetric key ratchet (abbrev. sk ratchet). It takes a key and some input data and produces a new key, as well as some output data. The new key is derived from the old key by using a so called Key Derivation Function. Repeating the process multiple times creates a Key Derivation Function Chain (KDF-Chain). The fact that it is impossible to reverse a key derivation is what gives the OMEMO protocol the property of Forward Secrecy.
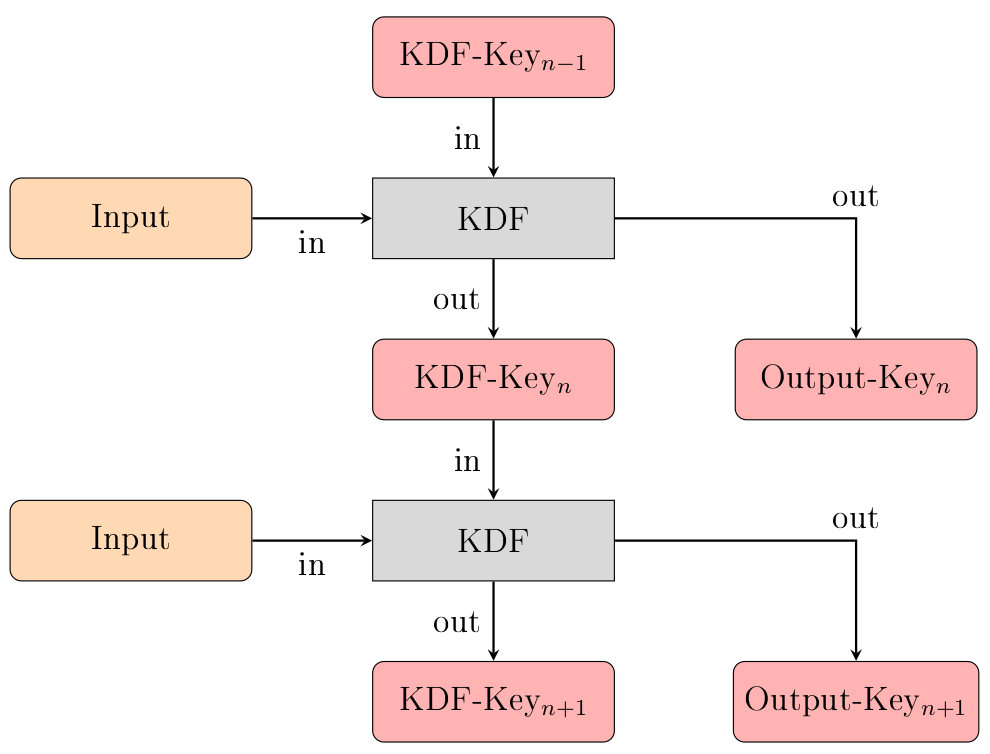
The above image illustrates the process of using a KDF-Chain to generate output keys from input data. In every step, the KDF-Chain takes the input and the current KDF-Key to generate the output key. Then it derives a new KDF-Key from the old one, replacing it in the process.
To summarize once again: Every time the KDF-Chain is used to generate an output key from some input, its KDF-Key is replaced, so if the input is the same in two steps, the output will still be different due to the changed KDF-Key.
One issue of this ratchet is, that it does not provide future secrecy. That means once an attacker gets access to one of the KDF-Keys of the chain, they can use that key to derive all following keys in the chain from that point on. They basically just have to turn the ratchet forwards.
Diffie-Hellman Ratchet
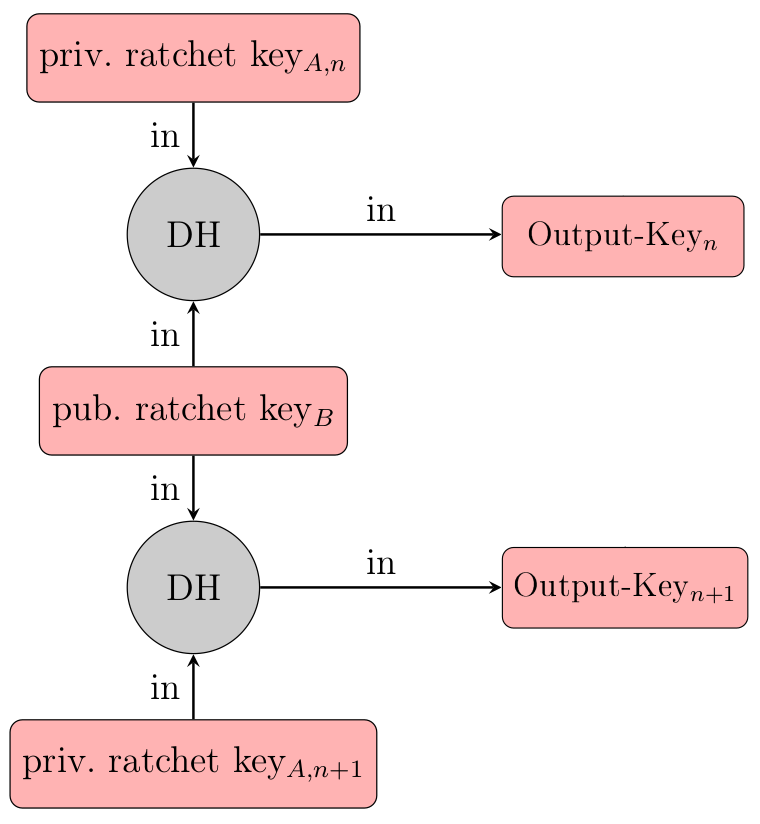
The second type of ratchet that we have to take a look at is the Diffie-Hellman Ratchet. This ratchet is basically a repeated Diffie-Hellman Key Exchange with changing key pairs. Every user has a separate DH ratcheting key pair, which is being replaced with new keys under certain conditions. Whenever one of the parties sends a message, they include the public part of their current DH ratcheting key pair in the message. Once the recipient receives the message, they extract that public key and do a handshake with it using their private ratcheting key. The resulting shared secret is used to reset their receiving chain (more on that later).
Once the recipient creates a response message, they create a new random ratchet key and do another handshake with their new private key and the senders public key. The result is used to reset the sending chain (again, more on that later).
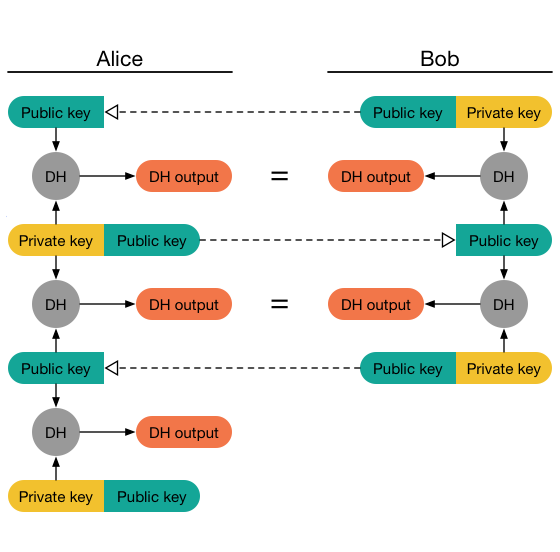
Image by OpenWhisperSystems (modified by author)
As a result, the DH ratchet is forwarded every time the direction of the message flow changes. The resulting keys are used to reset the sending-/receiving chains. This introduces future secrecy in the protocol.
Chains
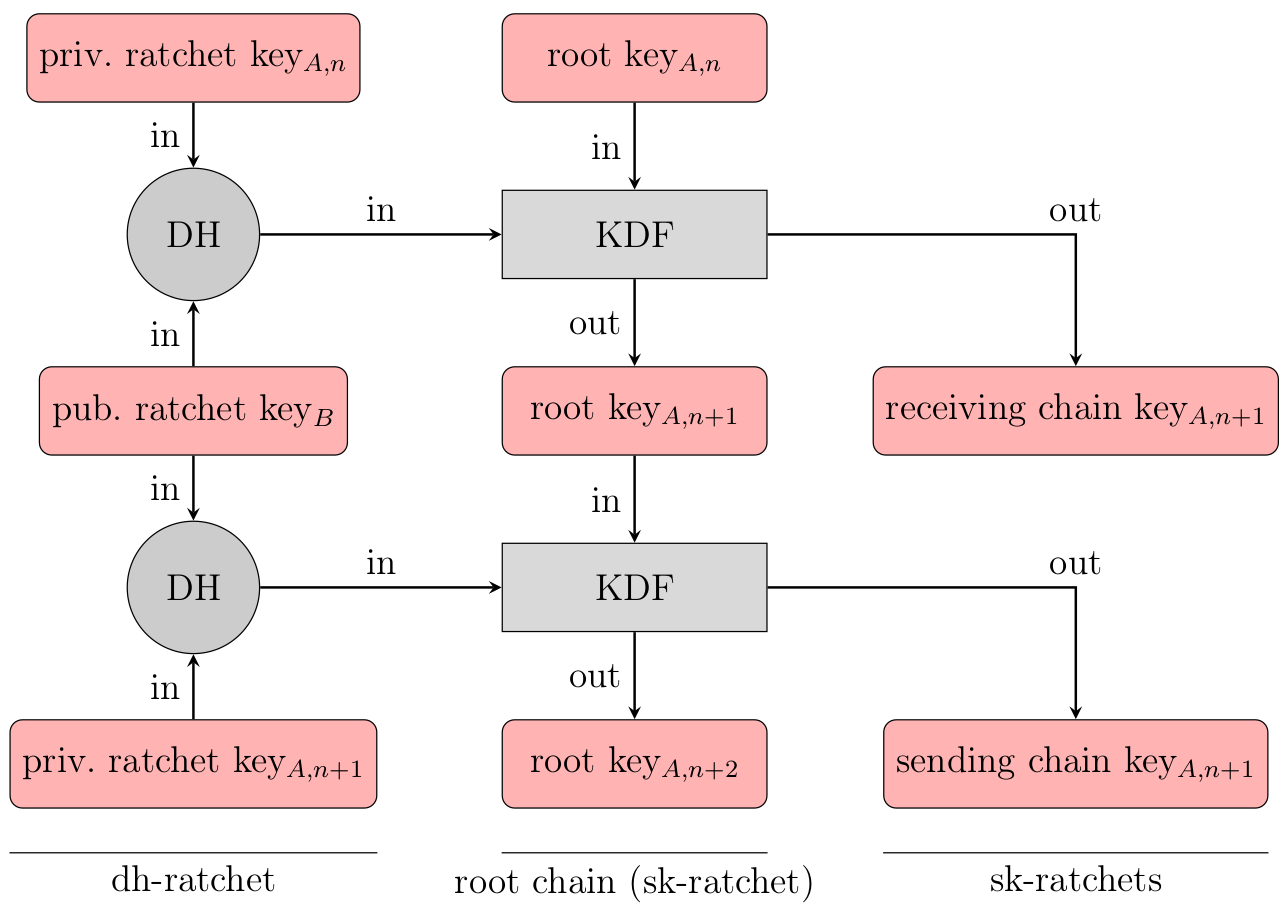
A session between two devices has three chains – a root chain, a sending chain and a receiving chain.
The root chain is a KDF chain which is initialized with the shared secret which was established using the X3DH handshake. Both devices involved in the session have the same root chain. Contrary to the sending and receiving chains, the root chain is only initialized/reset once at the beginning of the session.
The sending chain of the session on device A equals the receiving chain on device B. On the other hand, the receiving chain on device A equals the sending chain on device B. The sending chain is used to generate message keys which are used to encrypt messages. The receiving chain on the other hand generates keys which can decrypt incoming messages.
Whenever the direction of the message flow changes, the sending and receiving chains are reset, meaning their keys are replaced with new keys generated by the root chain.
An Example
I think this rather complex protocol is best explained by an example message flow which demonstrates what actually happens during message sending / receiving etc.
In our example, Obi-Wan and Grievous have a conversation. Obi-Wan starts by establishing a session with Grievous and sends his initial message. Grievous responds by sending two messages back. Unfortunately the first of his replies goes missing.
Session Creation
In order to establish a session with Grievous, Obi-Wan has to first fetch one of Grievous key bundles. He uses this to establish a shared secret S between him and Grievous by executing a X3DH key exchange. More details on this can be found in my previous post. He also extracts Grievous signed PreKey ratcheting public key. S is used to initialize the root chain.
Obi-Wan now uses Grievous public ratchet key and does a handshake with his own ratchet private key to generate another shared secret which is pumped into the root chain. The output is used to initialize the sending chain and the KDF-Key of the root chain is replaced.
Now Obi-Wan established a session with Grievous without even sending a message. Nice!
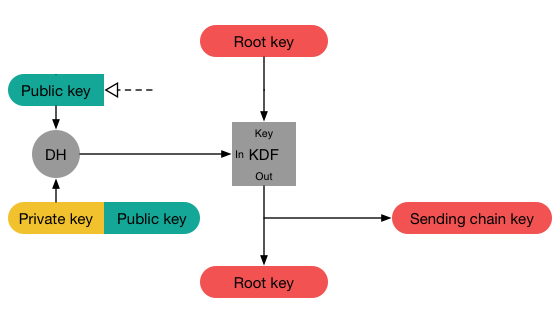
The initial root key comes from the result of the X3DH handshake.
Original image by OpenWhisperSystems (modified by author)
Initial Message
Now the session is established on Obi-Wans side and he can start composing a message. He decides to send a classy “Hello there!” as a greeting. He uses his sending chain to generate a message key which is used to encrypt the message.
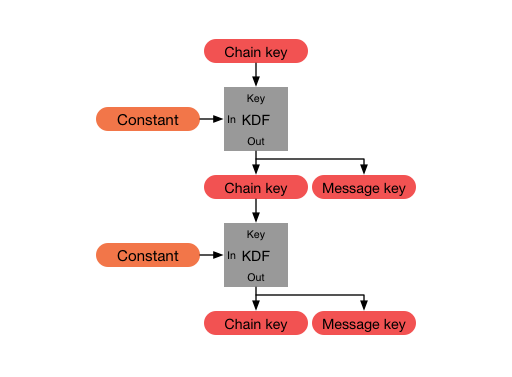
In our example only one message key is derived though.
Image by OpenWhisperSystems
Note: In the above image a constant is used as input for the KDF-Chain. This constant is defined by the protocol and isn’t important to understand whats going on.
Now Obi-Wan sends over the encrypted message along with his ratcheting public key and some information on what PreKey he used, the current sending key chain index (1), etc.
When Grievous receives Obi-Wan’s message, he completes his X3DH handshake with Obi-Wan in order to calculate the same exact shared secret S as Obi-Wan did earlier. He also uses S to initialize his root chain.
Now Grevious does a full ratchet step of the Diffie-Hellman Ratchet: He uses his private and Obi-Wans public ratchet key to do a handshake and initialize his receiving chain with the result. Note: The result of the handshake is the same exact value that Obi-Wan earlier calculated when he initialized his sending chain. Fantastic, isn’t it? Next he deletes his old ratchet key pair and generates a fresh one. Using the fresh private key, he does another handshake with Obi-Wans public key and uses the result to initialize his sending chain. This completes the full DH ratchet step.
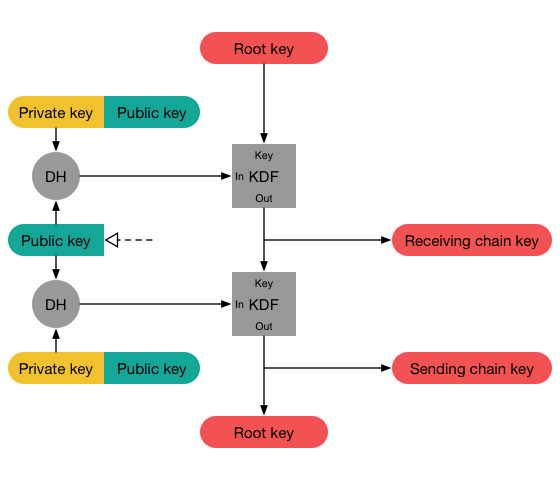
Image by OpenWhisperSystems
Decrypting the Message
Now that Grievous has finalized his side of the session, he can go ahead and decrypt Obi-Wans message. Since the message contains the sending chain index 1, Grievous knows, that he has to use the first message key generated from his receiving chain to decrypt the message. Because his receiving chain equals Obi-Wans sending chain, it will generate the exact same keys, so Grievous can use the first key to successfully decrypt Obi-Wans message.
Sending a Reply
Grievous is surprised by bold actions of Obi-Wan and promptly goes ahead to send two replies.
He advances his freshly initialized sending chain to generate a fresh message key (with index 1). He uses the key to encrypt his first message “General Kenobi!” and sends it over to Obi-Wan. He includes his public ratchet key in the message.
Unfortunately though the message goes missing and is never received.
He then forwards his sending chain a second time to generate another message key (index 2). Using that key he encrypt the message “You are a bold one.” and sends it to Obi-Wan. This message contains the same public ratchet key as the first one, but has the sending chain index 2. This time the message is received.
Receiving the Reply
Once Obi-Wan receives the second message and does a full ratchet step in order to complete his session with Grevious. First he does a DH handshake between his private and the Grevouos’ public ratcheting key he got from the message. The result is used to setup his receiving chain. He then generates a new ratchet key pair and does a second handshake. The result is used to reset his sending chain.
Obi-Wan notices that the sending chain index of the received message is 2 instead of 1, so he knows that one message must have been missing or delayed. To deal with this problem, he advances his receiving chain twice (meaning he generates two message keys from the receiving chain) and caches the first key. If later the missing message arrives, the cached key can be used to successfully decrypt the message. For now only one message arrived though. Obi-Wan uses the generated message key to successfully decrypt the message.
Conclusions
What have we learned from this example?
Firstly, we can see that the protocol guarantees forward secrecy. The KDF-Chains used in the three chains can only be advanced forwards, and it is impossible to turn them backwards to generate earlier keys. This means that if an attacker manages to get access to the state of the receiving chain, they can not decrypt messages sent prior to the moment of attack.
But what about future messages? Since the Diffie-Hellman ratchet introduces new randomness in every step (new random keys are generated), an attacker is locked out after one step of the DH ratchet. Since the DH ratchet is used to reset the symmetric ratchets of the sending and receiving chain, the window of the compromise is limited by the next DH ratchet step (meaning once the other party replies, the attacker is locked out again).
On top of this, the double ratchet algorithm can deal with missing or out-of-order messages, as keys generated from the receiving chain can be cached for later use. If at some point Obi-Wan receives the missing message, he can simply use the cached key to decrypt its contents.
This self-healing property was eponymous to the Axolotl protocol (an earlier name of the Signal protocol, the basis of OMEMO).
Acknowledgements
Thanks to syndace and paul for their feedback and clarification on some points.


11 responses to “Closer Look at the Double Ratchet”
[…] This is the first part of a small series about the cryptographic building blocks of OMEMO. This post is about the Extended Triple Diffie Hellman Key Exchange Algorithm (X3DH) which is used to establish a session between OMEMO devices.Part 2: Closer Look at the Double Ratchet […]
@vanitasvitae the web page isn't loading, it spins for a long time
@vanitasvitae> As a result, the DH ratchet is forwarded every time the direction of the message flow changes. The resulting keys are used to reset the sending-/receiving chains. This introduces future secrecy in the protocol.How does this introduce forward secrecy?
@vanitasvitae @neetx @neetx
c|_|
@vanitasvitaeRight on time, I discovered OMEMO and Double Ratchet just yesterday. Thanks for the write up.
Yep The resulting keys are used to reset the sending-/receiving chains. This introduces future secrecy in the protocol.How does this introduce forward secrecy?
Forward Secrecy is given by the chains themselves. New keys are derived from older keys but you cannot guess the older keys, given only the new keys.
[…] chiffrée avec un interlocuteur même s’il est hors-ligne. Dans son deuxième article, il se penche de plus près sur le double ratchet qui protège la confidentialité des sessions de discussion passées et futures même si une […]
Thanks for taking the time to write this down in (relatively) easy to understand language.
I think my head is a few degrees warmer after having read this 🙂
You’re welcome 🙂