This is part 2 of a small series on verifying the validity of packet sequences using tools from theoretical computer science. Read part 1 here.

In the previous blog post I discussed how a formal grammar can be transformed into a pushdown automaton in order to check if a sequence of packets or tokens is part of the language described by the grammar. In this post I will discuss how I implemented said automaton in Java in order to validate OpenPGP messages in PGPainless.

In the meantime, I made some slight changes to the automaton and removed some superfluous states. My current design of the automaton looks as follows:

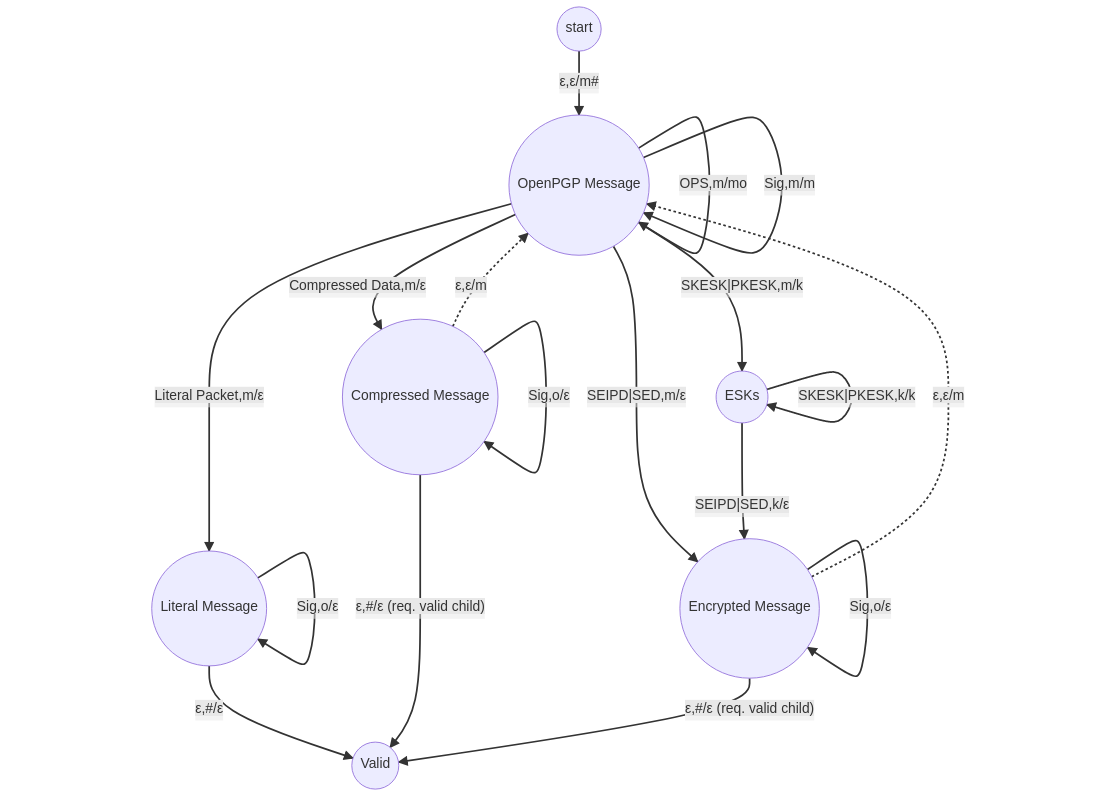
If you compare this diagram to the previous iteration, you can see that I got rid of the states “Signed Message”, “One-Pass-Signed Message” and “Corresponding Signature”. Those were states which had ε-transitions to another state, so they were not really useful.

For example, the state “One-Pass-Signed Message” would only be entered when the input “OPS” was read and ‘m’ could be popped from the stack. After that, there would only be a single applicable rule which would read no input, pop nothing from the stack and instead push back ‘m’. Therefore, these two rule could be combined into a single rule which reads input “OPS”, pops ‘m’ from the stack and immediately pushes it back onto it. This rule would leave the automaton in state “OpenPGP Message”. Both automata are equivalent.

One more minor detail: Since I am using Bouncy Castle, I have to deal with some of its quirks. One of those being that BC bundles together encrypted session keys (PKESKs/SKESKs) with the actual encrypted data packets (SEIPD/SED). Therefore when implementing, we can further simplify the diagram by removing the SKESK|PKESK parts:

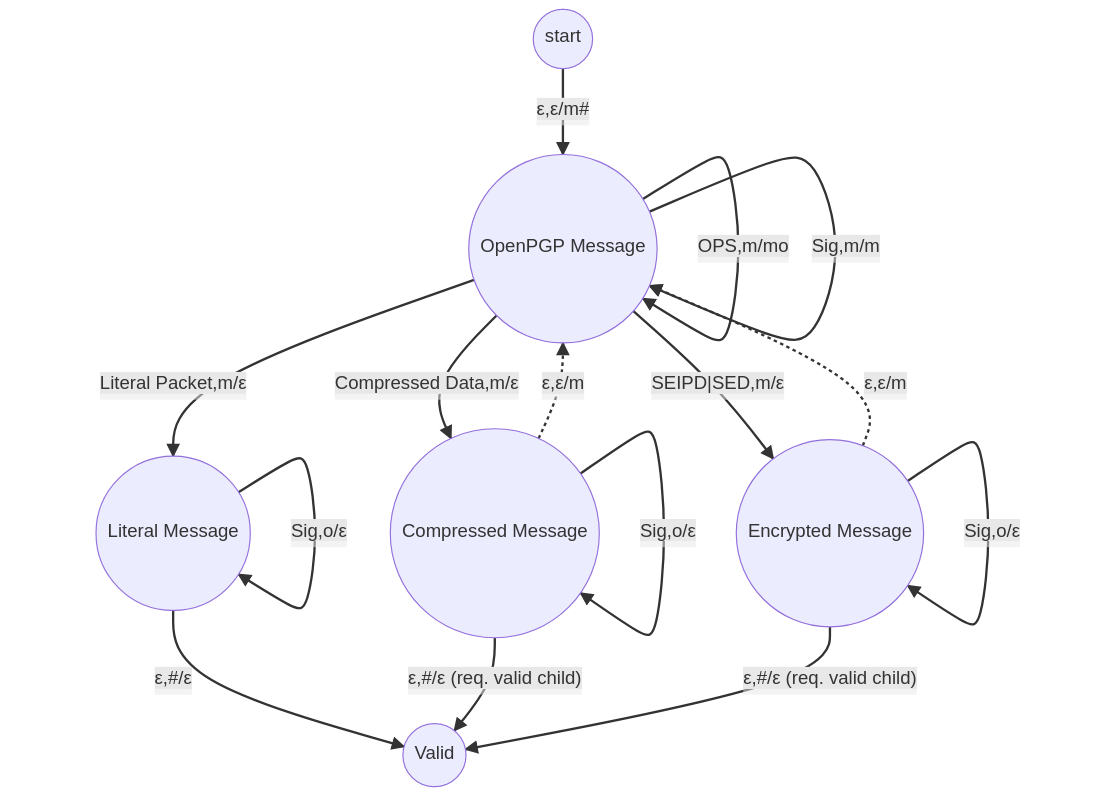
Now, in order to implement this automaton in Java, I decided to define enums for the input and stack alphabets, as well as the states:

public enum InputAlphabet {
    LiteralData,
    Signature,            // Sig
    OnePassSignature,     // OPS
    CompressedData,
    EncryptedData,        // SEIPD|SED
    EndOfSequence         // End of message/nested data
}

public enum StackAlphabet {
    msg,                 // m
    ops,                 // o
    terminus             // #
}

public enum State {
    OpenPgpMessage,
    LiteralMessage,
    CompressedMessage,
    EncryptedMessage,
    Valid
}

Note, that there is no “Start” state, since we will simply initialize the automaton in state OpenPgpMessage, with ‘m#’ already put on the stack.

We also need an exception class that we can throw when OpenPGP packet is read when its not allowed. Therefore I created a MalformedOpenPgpMessageException class.

Now the first design of our automaton itself is pretty straight forward:

public class PDA {
    private State state;
    private final Stack<StackAlphabet> stack = new Stack<>();
    
    public PDA() {
        state = State.OpenPgpMessage;    // initial state
        stack.push(terminus);            // push '#'
        stack.push(msg);                 // push 'm'
    }

    public void next(InputAlphabet input)
            throws MalformedOpenPgpMessageException {
        // TODO: handle the next input packet
    }

    StackAlphabet popStack() {
        if (stack.isEmpty()) {
            return null;
        }
        return stack.pop();
    }

    void pushStack(StackAlphabet item) {
        stack.push(item);
    }

    boolean isEmptyStack() {
        return stack.isEmpty();
    }

    public boolean isValid() {
        return state == State.Valid && isEmptyStack();
    }
}

As you can see, we initialize the automaton with a pre-populated stack and an initial state. The automatons isValid() method only returns true, if the automaton ended up in state “Valid” and the stack is empty.

Whats missing is an implementation of the transition rules. I found it most straight forward to implement those inside the State enum itself by defining a transition() method:

public enum State {

    OpenPgpMessage {
        @Overrides
        public State transition(InputAlphabet input, PDA automaton)
                throws MalformedOpenPgpMessageException {
            StackAlphabet stackItem = automaton.popStack();
            if (stackItem != OpenPgpMessage) {
                throw new MalformedOpenPgpMessageException();
            }
            swith(input) {
                case LiteralData:
                    // Literal Packet,m/ε
                    return LiteralMessage;
                case Signature:
                    // Sig,m/m
                    automaton.pushStack(msg);
                    return OpenPgpMessage;
                case OnePassSignature:
                    // OPS,m/mo
                    automaton.push(ops);
                    automaton.push(msg);
                    return OpenPgpMessage;
                case CompressedData:
                    // Compressed Data,m/ε
                    return CompressedMessage;
                case EncryptedData:
                    // SEIPD|SED,m/ε
                    return EncryptedMessage;
                case EndOfSequence:
                default:
                    // No transition
                    throw new MalformedOpenPgpMessageException();
            }
        }
    },

    LiteralMessage {
        @Overrides
        public State transition(InputAlphabet input, PDA automaton)
                throws MalformedOpenPgpMessageException {
            StackAlphabet stackItem = automaton.popStack();
            switch(input) {
                case Signature:
                    if (stackItem == ops) {
                        // Sig,o/ε
                        return LiteralMessage;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                case EndOfSequence:
                    if (stackItem == terminus && automaton.isEmptyStack()) {
                        // ε,#/ε
                        return valid;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                default:
                    throw new MalformedOpenPgpMessageException();
            }
        }
    },

    CompressedMessage {
        @Overrides
        public State transition(InputAlphabet input, PDA automaton)
                throws MalformedOpenPgpMessageException {
            StackAlphabet stackItem = automaton.popStack();
            switch(input) {
                case Signature:
                    if (stackItem == ops) {
                        // Sig,o/ε
                        return CompressedMessage;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                case EndOfSequence:
                    if (stackItem == terminus && automaton.isEmptyStack()) {
                        // ε,#/ε
                        return valid;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                default:
                    throw new MalformedOpenPgpMessageException();
            }
        }
    },

    EncryptedMessage {
        @Overrides
        public State transition(InputAlphabet input, PDA automaton)
                throws MalformedOpenPgpMessageException {
            StackAlphabet stackItem = automaton.popStack();
            switch(input) {
                case Signature:
                    if (stackItem == ops) {
                        // Sig,o/ε
                        return EncryptedMessage;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                case EndOfSequence:
                    if (stackItem == terminus && automaton.isEmptyStack()) {
                        // ε,#/ε
                        return valid;
                    } else {
                        throw new MalformedOpenPgpMessageException();
                    }
                default:
                    throw new MalformedOpenPgpMessageException();
            }
        }
    },

    Valid {
        @Overrides
        public State transition(InputAlphabet input, PDA automaton)
                throws MalformedOpenPgpMessageException {
            // Cannot transition out of Valid state
            throw new MalformedOpenPgpMessageException();
        }
    }
    ;

    abstract State transition(InputAlphabet input, PDA automaton)
            throws MalformedOpenPgpMessageException;
}

It might make sense to define the transitions in an external class to allow for different grammars and to remove the dependency on the PDA class, but I do not care about this for now, so I’m fine with it.

Now every State has a transition() method, which takes an input symbol and the automaton itself (for access to the stack) and either returns the new state, or throws an exception in case of an illegal token.

Next, we need to modify our PDA class, so that the new state is saved:

public class PDA {
    [...]

    public void next(InputAlphabet input)
            throws MalformedOpenPgpMessageException {
        state = state.transition(input, this);
    }
}

Now we are able to verify simple packet sequences by feeding them one-by-one to the automaton:

// LIT EOS
PDA pda = new PDA();
pda.next(LiteralData);
pda.next(EndOfSequence);
assertTrue(pda.isValid());

// OPS LIT SIG EOS
pda = new PDA();
pda.next(OnePassSignature);
pda.next(LiteralData);
pda.next(Signature);
pda.next(EndOfSequence);
assertTrue(pda.isValid());

// COMP EOS
PDA pda = new PDA();
pda.next(CompressedData);
pda.next(EndOfSequence);
assertTrue(pda.isValid());

You might say “Hold up! The last example is a clear violation of the syntax! A compressed data packet alone does not make a valid OpenPGP message!”.

And you are right. A compressed data packet is only a valid OpenPGP message, if its decompressed contents also represent a valid OpenPGP message. Therefore, when using our PDA class, we need to take care of packets with nested streams separately. In my implementation, I created an OpenPgpMessageInputStream, which among consuming the packet stream, handling the actual decryption, decompression etc. also takes care for handling nested PDAs. I will not go into too much details, but the following code should give a good idea of the architecture:

public class OpenPgpMessageInputStream {
    private final PDA pda = new PDA();
    private BCPGInputStream pgpIn = ...; // stream of OpenPGP packets
    private OpenPgpMessageInputStream nestedStream;

    public OpenPgpMessageInputStream(BCPGInputStream pgpIn) {
        this.pgpIn = pgpIn;
        switch(pgpIn.nextPacketTag()) {
            case LIT:
                pda.next(LiteralData);
                ...
                break;
            case COMP:
                pda.next(CompressedData);
                nestedStream = new OpenPgpMessageInputStream(decompress());
                ...
                break;
            case OPS:
                pda.next(OnePassSignature);
                ...
                break;
            case SIG:
                pda.next(Signature);
                ...
                break;
            case SEIPD:
            case SED:
                pda.next(EncryptedData);
                nestedStream = new OpenPgpMessageInputStream(decrypt());
                ...
                break;
            default:
                // Unknown / irrelevant packet
                throw new MalformedOpenPgpMessageException();
    }

    boolean isValid() {
        return pda.isValid() &&
               (nestedStream == null || nestedStream.isValid());

    @Override
    close() {
        if (!isValid()) {
            throw new MalformedOpenPgpMessageException();
        }
        ...
    }
}

The key thing to take away here is, that when we encounter a nesting packet (EncryptedData, CompressedData), we create a nested OpenPgpMessageInputStream on the decrypted / decompressed contents of this packet. Once we are ready to close the stream (because we reached the end), we not only check if our own PDA is in a valid state, but also whether the nestedStream (if there is one) is valid too.

This code is of course only a rough sketch and the actual implementation is far more complex to cover many possible edge cases. Yet, it still should give a good idea of how to use pushdown automata to verify packet sequences 🙂 Feel free to check out my real-world implementation here and here.

Happy Hacking!