The week of the first evaluation phase is here. This is the fourth week of GSoC – wow, time flew by quite fast this year 🙂
This week I plan to switch my OX implementation over to PGPainless in order to have a working prototype which can differentiate between sign, crypt and signcrypt elements. This should be pretty straight forward. In case everything goes wrong, I’ll keep the current implementation as a working backup solution, so we should be good to go 🙂
OpenPGP Key Type Considerations
I spent some time testing my OpenPGP library PGPainless and during testing I noticed, that messages encrypted and signed using keys from the family of elliptic curve cryptography were substantially smaller than messages encrypted with common RSA keys. I knew already, that one benefit of elliptic curve cryptography is, that the keys can be much smaller while providing the same security as RSA keys. But what was new to me is, that this also applies to the length of the resulting message. I did some testing and came to interesting results:
In order to measure the lengths of produced cipher text, I create some code that generates two sets of keys and then encrypts messages of varying lengths. Because OpenPGP for XMPP: Instant Messaging only uses messages that are encrypted and signed, all messages created for my tests are encrypted to, and signed with one key. The size of the plaintext messages ranges from 20 bytes all the way up to 2000 bytes (1000 chars).
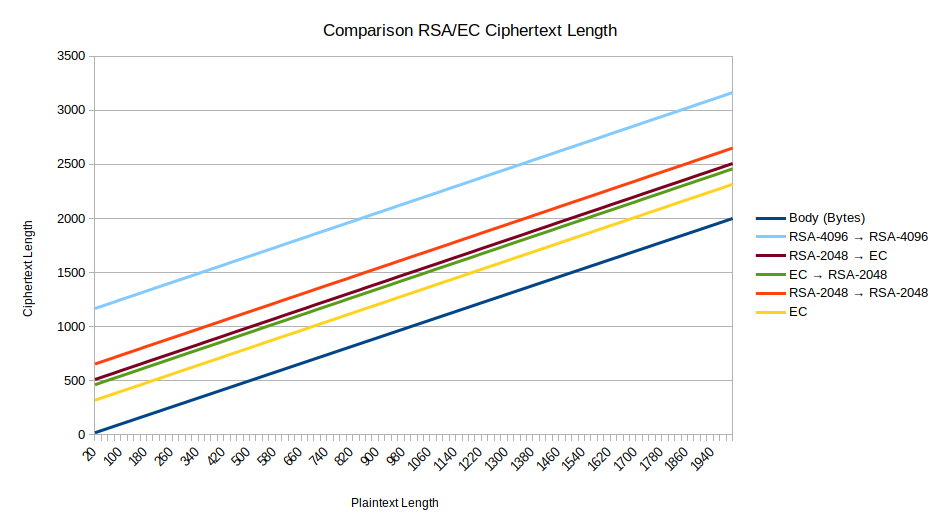
The resulting diagram shows, how quickly the size of OpenPGP encrypted messages explodes. Lets assume we want to send the smallest possible OX message to a contact. That message would have a body of less than 20 bytes (less than 10 chars). The body would be encapsulated in a signcrypt-element as specified in XEP-0373. I calculated that the length of that element would be around 250 chars, which make 500 bytes. 500 bytes encrypted and signed using 4096 bit RSA keys makes 1652 bytes ciphertext. That ciphertext is then base64 encoded for transport (a rule of thumb for calculating base64 size is ceil(bytes/3) * 4 which results in 2204 bytes. Those bytes are then encapsulated in an openpgp-element (adds another 94 bytes) which can be appended to a message. All in all the openpgp-element takes up 2298 bytes, compared to a normal body, which would only take up around 46 bytes.
So how do elliptic curves come to the rescue? Lets assume we send the same message again using 256 bit ECC keys on the curve P-256. Again, the length of the signcrypt-element would be 250 chars or 500 bytes in the beginning. OpenPGP encrypting those bytes leads to 804 bytes of ciphertext. Applying base64 encoding results in 1072 bytes, which finally make 1166 bytes of openpgp-element. Around half the size of an RSA encrypted message.
For comparison: I estimated a typical XMPP chat message body to be around 70 characters or 140 bytes based on a database dump of my chat client.
We must not forget however, that the stanza size follows a linear function of the form y = m*x+b, so if the plaintext size grows, the difference between RSA and ECC will become less and less significant.
Looking at the data, I noticed, that applying OpenPGP encryption always added a constant number to the size of the plaintext. Using 256 bit ECC keys only adds around 300 bytes, encrypting a message using 2048 bit RSA keys adds ~500 bytes, while RSA with 4096 bits adds 1140 bytes. The formula for my setup would therefore be y = x + b, where x and y are the size of the message before and after applying encryption and b is the overhead added. This formula doesn’t take base64 encoding into consideration. Also, if multiple participants -> multiple keys are involved, the formula is suspected to underestimate, as the overhead will grow further.
One could argue, that using smaller RSA keys would reduce the stanza size as well, although not as much, but remember, that RSA keys have to be big to be secure. An 3072 bit RSA key provides the same security as an 256 bit ECC key. Quoting Wikipedia:
The NIST recommends 2048-bit keys for RSA. An RSA key length of 3072 bits should be used if security is required beyond 2030.
As a conclusion, I propose to add a paragraph to XEP-0373 suggesting the use of ECC keys to keep the stanza size low.


One response to “Summer of Code: Evaluation and Key Lengths”
[…] also proud of my posting from June 11, in which I investigated OpenPGP message lengths depending on which key types are […]